Ставка дисконтирования r введена в формулы (2
– 4) с подстрочным индексом i, что означает необходимость прогнозирования ее
величины для каждого года осуществления проекта в отдельности. С теоретической
точки зрения данный подход является наиболее обоснованным, так как даже
безрисковая доходность самых надежных финансовых инструментов (например,
государственных облигаций) не остается неизменной во времени. Ставки дохода по
краткосрочным безрисковым обязательствам могут отличаться от соответствующих
ставок для более длительных финансовых инструментов (обычно, ставки растут по
мере удлинения срока до погашения соответствующих ценных бумаг, но данная
закономерность может нарушаться). Процентные ставки, отражающие сегодняшнюю
оценку ожидаемой инвесторами доходности по безрисковым инструментам различной
длительности, называются спот-ставками.
Например, доходность трехмесячных векселей Казначейства США может составлять
1,7% годовых, в то время как по своим десятилетним облигациям американское
правительство готово выплачивать около 4% годовых (данное соотношение было
характерно для второй половины 2004 г.).
Изменения уровня безрисковой ставки в
зависимости от длительности срока, остающегося до погашения соответствующего
финансового инструмента, называется кривой
спот-ставок, которая, как уже отмечалось выше, обычно направлена вверх по
мере удлинения сроков к погашению, хотя нередки и исключения из данного
правила. Для целей инвестиционного планирования наличие такой закономерности
означает необходимость прогнозирования спот ставок для каждого года реализации
проекта в отдельности. Например, для первого года должна использоваться годовая
спот-ставка, для второго – двухлетняя и т.д. Однако на практике данный подход
почти не используется, вместо набора спот-ставок ri в формулу расчета NPV
обычно подставляется единая ставка дисконтирования r, усредняющая различия,
вытекающие из неоднородности временной структуры процентных ставок.
Данный унифицированный показатель (r) отражает
для предприятия цену (альтернативные издержки), которую ему приходится платить
инвесторам для привлечения капитала. Иными словами, предполагается, что
инвесторы рассчитывают получить от данного предприятия доход на свои вложения,
величина которого не ниже r. Соответственно, использование предприятием
полученного у инвесторов капитала (реализация инвестиционного проекта) также
должна обеспечить некую среднюю
доходность, равную или превышающую r. Поэтому, в формуле расчета NPV вместо
набора спот-ставок, как правило, используют единый показатель средней ожидаемой
доходности (цены капитала) r:
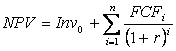 (5)
(5)
Например, первоначальные инвестиции по
трехлетнему проекту составляют 50 млн. руб., в течение первого года свободный
денежный поток от его реализации составит 10 млн. руб., за второй год проект
принесет 20, а за третий 25 млн. руб. Ставка дисконтирования составляет 5%
годовых. График денежных потоков по проекту будет иметь следующий вид:
Годы 0 1 2 3
Денежные потоки -50 10 20 25
Подставляя эти данные в выражение (5),
получим:
NPV = -50 + 10 / (1 + 0,05)1 + 20 / (1 +
0,05)2 + 25 / (1 + 0,05)3 = -0,74 млн. руб.
То есть, чистая приведенная стоимость данного
проекта отрицательна, поэтому его не следует принимать к реализации.
Следствием переноса внимания от использования
набора спот-ставок к среднему за пери-од значению стало появление возможности
расчета еще одного интересного финансового показателя – внутренней нормы доходности (Internal Rate of Return – IRR) –
название которого в различных источниках переводится как внутренняя ставка
прибыли, внутренняя ставка рентабельности или внутренняя процентная ставка.
Этот показатель представляет собой такую величину средней процентной ставки,
использование которой в уравнении (5) приравнивает (по абсолютной величине)
левую часть этого выражения к его правой части. Иными словами, дисконтирование
будущих денежных потоков по ставке, равной IRR, обеспечивает получение нулевой
чистой приведенной стоимости. Формально это можно отобразить следующим образом:
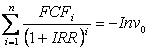 или
или
 (6)
(6)
(при условии, что суммы денежных оттоков (Inv0)
изначально отражаются со знаком «минус»).
Техника расчета IRR также была подробно
рассмотрена в лекции о временной стоимости денег, поэтому здесь мы просто
приведем значение этого показателя, найденное для рассмотренного нами выше условного
примера: IRR (-50; 10; 20; 25) = 4,31%. (Для расчета этого показателя можно
использовать встроенную финансовую функцию табличного процессора Excel, которая
в русскоязычной версии этой программы обозначается как ВНДОХ (ВСД в более
поздних версиях), а в английском варианте имеет уже знакомое нам обозначение
IRR).
Вернуться
на предыдущую страницу
Вернуться
к списку всех лекций